CNN 의 구조나 학습 과정이나 그런 거는 이해하기 쉬운데, 구체적으로 모델이 어떻게 학습하고 어떻게 feature를 추출하는지 우리로서는 알기 쉽지 않다. 또한 그런 관점에서 이런 DNN들을 비판하는 목소리도 꽤 있었다고 한다. (현재도 그런지는 잘 모르겠다) 그래서 이제 필터를 통해서 모델이 구체적으로 어떤 걸 학습하고 있는지 열어보자! 그런게 이제 컴퓨터 비전에서 visualizing and understanding 분야라고 생각하면 될 것 같다.
이 논문의 핵심은 이해가 쉽다. 하지만 그 디테일이 이해가 쉽지 않다. 그래서 초록이 거의 내가 완벽하게 이해한 부분 마지막 부분이라고 할 수 있따ㅜㅜ
기본이 되는 용어들을 많이 사용해서 어려웠다. 예를 들면 feature, unit, feature space, random direction 사실 이 포스팅을 하는 지금도 완벽하게 이해하지 못했다. 그래서 넘나리 답답하다ㅠㅠ 이해를 못했는데 글을 쓰는 것도 지옥이다! 그래서 이것저것 검색을 많이 해봤는데 뭔가 통일된 답안을 내놓지 않는 인터넷이라 답답했다.
=> 사족의 결론: 블로그 포스팅 올라온 논문 + 올리지 않았지만 읽은 논문 중에서 제일 이해를 못 함
이제 사족 끝
Intriguing properties of neural networks
초록 Abstract
DNN 은 neural network를 통해서 함수들을 근사할 수 있다는 점에서 expressive 하다. 1 그 대신 우리가 직관적으로 이해할 수 없는 속성을 이용해 해석할 수 없는 solution을 내놓기도 한다. 따라서 본 논문에서는 크게 2가지의 속성을 소개하고자 한다.
첫번째 속성은 high level의 유닛 하나하나와 그런 high level의 유닛을 랜덤하게 선형결합을 한 것 사이에는 차이가 없었다는 실험 결과에서 기인한다. 즉 이를 통해서 알 수 있는 것은 개별적인 유닛이 아니라 그 공간에서 semnatic information이 있다는 것이다.
두번째 속성은 input-output의 매핑이 상당히 불연속적이라는 실험결과에서 기인한다. 즉 특정 학습 데이터로 학습시킨 특정 구조의 모델에서 생성한 적대적 학습 데이터는 다른 학습 데이터, 다른 구조의 모델을 이용했을 때도 예측에 난항을 겪는다.
[두 가지의 counter intuitive properties]
1. semantic meaning of individual unit 과 관련된 속성으로, 개별적인 유닛 그 자체에는 semantic information이 없다.
2. 인풋에 작은 변형을 만들었을 때(adversarial example) neural network의 안정성과 관련된 속성으로, 놀랍게도 다른 학습 데이터 다른 구조의 모델로 이 adversarial example은 대게 예측이 잘 안 되었다.
[Notation/Experiment Detail]
- Notation
$x \in \mathbb{R}^{m}$ : input image
$\phi$ : activation values of some layer
- Experiment detail
총 세 가지의 데이터 셋을 이용, 각각 다른 구조의 모델을 이용했다.
- MNIST 데이터 셋 + FC (1 이상의 은닉층과 소프트맥스 분류의 구조 )/ AE(오토인코더)
- ImageNet 데이터 셋 + AlexNet
- YOUTUBE 데이터 셋 + QuocNet(비지도 학습을 이용한 네트워크)
(*오토인코더 이거 이미지 생성 쪽 공부할 때 봤었다. 이게 수학으로 이해하기에는 최고봉으로 어렵다고..
https://www.youtube.com/watch?v=o_peo6U7IRM&t=5491s 이거는 네이버!! 에서 하는 강의? 인데
한 다섯시간 동안 오토인코더만 다룬다ㅎㅎ 관심 있으면 보길 바란다.
나도 넘나리 궁금해서 보고 싶다. 시간만 나면...ㅠㅠ)
이때 MNIST 데이터 셋은 서로 배타적인 $P_{1}, P_{2}$로 나누어서 학습을 하는데 자세한 디테일은 추후 section에서 확인할 수 있다.
[semantic meaning of individual unit]
These works interpret an activation of a hidden unit as a meaningful feature. They look for input images which maximize the activation value of this single feature.
각각의 유닛이 어떤 의미론적 정보를 갖고 있는지와 관련된 선행 연구들은 각 피쳐의 활성화 값을 최대화하는 인풋 이미지를 찾았다고 한다. 이게 무슨 말이냐.. 수식으로 바꿔보자
$x^{'} = argmax_{x\in L} <\phi (x), e_{i}>$
이때 L은 모델을 학습할 때 사용하지 않았던 이미지 데이터 셋이다.
한편 $e_{i}$는 i번째 은닉층 유닛과 관련된 natural/standard 기저 벡터다.
본 논문에서는 랜덤 direction 벡터를 생성해서 위의 결과값과 비교해보고자 했다.
랜덤 direction 백터를 이용해서
$x^{'} = argmax_{x\in L} <\phi (x), \upsilon>$
위와 같이 $x^{'}$을 계산한다.
 |
 |
 |
 |
위 그림들을 보면 어떤가?
우리는 각 유닛을 최대화하는 이미지들을 살펴봤고, 또 그냥 랜덤한 벡터를 최대화하는 이미지를 살펴봤다.
그랬더니 둘이 비슷한 속성을 캡쳐하는 것처럼 보였다.
그렇다면 유닛 자체에 정보들이 담겨있다기 보다는, 둘이 공유하는 것에 정보들이 담겨있다는 뜻이다.
무엇이 공통점인가?
둘의 space 라고 할 수 있겠다.
여기까지 공간에 우리가 이해할 수 있는 의미 있는 정보가 있다~ 는 속성을 살펴보았다.
(+ 서론에서는 개별 유닛과 개별 유닛의 컴비네이션을 비교했다고 했다. 개별 유닛의 컴비네이션? 그건 random direction인 $\upsilon$이라고 보면 된다. 왜냐하면 기저 벡터를 선형적으로 결합하면 그 공간의 모든 방향을 나타낼 수 있고 그 중에 하나가 우리가 생성한 $\upsilon$이기 때문이지! 물론 뇌피셜이지만 맞을 것 같다. 그리고 또 둘의 공통점이 space 라는 이야기도 결국 여기서 파생된다. 기저 벡터들의 결합으로 표현되는 space 속에 random direction이 있으니까? 결국 둘다 같은 space 에 있다는 말이다. )
[stability of neural networks with respect to small perturbation to their inputs]
앞서서 우리는 unit 수준에서 DNN을 이해해보았다. 그렇다면 이번엔 Global 한 레벨에서 DNN을 이해해보자.
이 Global 한 레벨에서 DNN을 이해하기 위한 연구에는 맞게 input의 어느 파트 때문에 이미지가 맞게 classifcation 되었는지 탐구하는 것 등이 포함된다. 이러한 연구들은 결국 인풋과 아웃풋 사이를 매핑에 대한 이해를 도와준다.
보통 output 레이어는 input 레이어의 비선형적 표현이다. 앞의 인공지능 뉴런 포스팅에서도 이야기를 했지만, 우리가 결국 은닉층을 많이 표현하는 것은 선형적으로 표현할 수 없는 XOR 게이트를 표현하기 위해서다. 그러니까 다층 퍼셉트론 내지 은닉층을 이용하는 건 비선형성을 도입하기 위해서이니, 당연히 input을 어떻게 선형적인 변환을 주어서 우리의 output을 구할 수는 없는 것이다.
이와 관련해 이렇게 깊은 non-linear 구조는 모델이 결국 같은 class의 개체이지만 다른 시점에서 보았다던지 등의 이유로 인해 조금 달라보이는 개체들이 포함된 지역에 낮은 class probability를 할당하게 할 수도 있다는 주장이 있었다. 즉 이 주장에는 "local generalization" 가 일어난다는 것이 내제되어 있는 셈이다.
그러니까 충분히 작은 $\epsilon$에 대해서 만약 ||r|| < $\epsilon$을 만족하는 r과 input 의 합, 그러니까 $x+r$ 는 그 모델에 의해서 정답인 class일 확률이 높게 된다는 주장이다. 수식으로 설명하면 그렇고. 말로는 위에서 말한 것의 반대로 생각하면 된다. 개체가 있는 region보다 $r$ 만큼 떨어진 region에도 해당 class를 높은 probability로 예측한다는 뜻이다.
하지만 본 연구에서는 그게 아니라고 말한다.
나도 이 부분이 제일 신기했다.

가장 왼쪽 col 은 ImageNet의 데이터 이다. 이거를 모델에 학습시킬 때 (첫번째 row를 예로 들 때) 원래 정답인 차 대신에 타조 로 정답 값을 내도록 input에 변형을 해준다. (이때 이런 변형을 우리가 눈으로 보기에는 눈치 못챌 정도이다.) 가장 오른쪽 col은 이렇게 변형된, 즉 adversarial examples이다. 육안으로 보기에는 아무런 차이가 없어보이지만, 컴퓨터는 정답이 아닌, 다른 레이블로 학습된 상태이다.
(+ 그리고 기존 연구들에서 원본 이미지를 조금씩 바꿔서 학습함으로써 모델의 수렴 속도를 높이거나 이제 robustness 를 증가시키려고 하는데. 이런 것들이 사실은 비효율적이라고 한다. 왜냐하면 원본 이미지와 상관성이 높기 때문이고, 어쨌든 그렇게 변형된 것들이 모두 기존의 학습 데이터 셋 분포에서 나온 것이기 때문이다. )
[그렇다면 어떻게 adversarial example을 만들 것인가??]
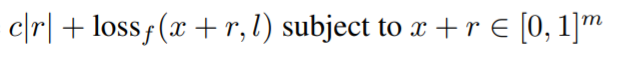
을 최소화하는 r을 찾는 다고 한다. 저기서 빠진 조건 하나는 f(x+r) = l 이다.
f는

이런 함수로, 이미지를 레이블로 메핑하는 함수인 셈이다.
그러니까 f(x+r) = l 은 다른 region인 x+r에 대해서도 여전히 정답인 class l 로 예측은 한다는 조건이다.
위의 최소화하는 식은 convex 하면 구하기 쉽지만 그렇지 않기 때문에 근사값을 구하기 위해서 L-BFGS 를 이용한다고 한다. 이 방법은 아무래도 적대적 기계 학습과 관련이 있는 것 같다. 아는 분이 이거 책 쓰셨던데 알려주셨으면 좋겠다
[만든 적대적 예제를 어떻게 이용할 것인가?]
크게 두 가지 과정이 있다. (1) cross model generalization (2) cross training-set generalization
이 과정을 통해서 보여주고 싶은 것은 이런 adversarial example들이 학습한 모델뿐 아니라 다른 모델, 다른 데이터 셋을 이용했을 때도 여전히 잘 분류를 못한다는 것을 보여줌으로써 이것이 단순히 과적합의 문제가 아니라는 것이다.
- cross model generalization

train,test는 데이터 셋에 아무 처리를 안 했을 때 나오는 순수한 학습/검증 오류 값이다. 그리고 옆에 있는 Av.min.distortion은 모든 데이터를 misclassify 하게 하는 왜곡의 정도이다.
이 왜곡의 정도는
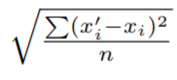
이 식을 따라 측정한다.
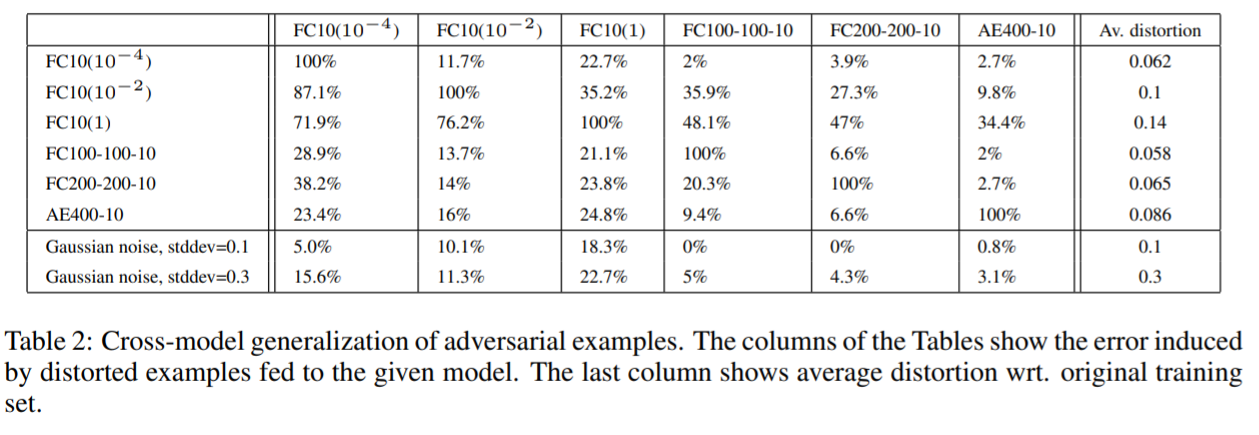
결과는 위의 그림과 같다. 대각원소를 보면 다 100% 이다. 이게 뭐냐면 각 모델에 맞게 다 missclassify 하도록 적대적 예제를 생성했으니, 그것들은 다 missclassify 되는 것이다.
예를 들어서 보면 FC10($10^{-4}$)의 모델에서는 다 missclassify 된 적대적 예제가 FC10($10^{-2}$)의 구조로 학습된 모델에서는 약 11.7%를 잘못 classify 했다는 말이다.
전체적으로 보면 오토인코더가 가장 성능이 좋지만. 그래도 여전히 한 모델에서 missclassify 되는 데이터가 다른 모델에서도 missclassify 된다는 사실을 알 수 있다.
- cross training-set generalization
그리고 이번에는 서로 다른 데이터 셋으로 훈련시키고 여전히 adversarial example이 missclassify 되는지 확인했다.

위의 Table 1과 동일한 내용을 표현한다.
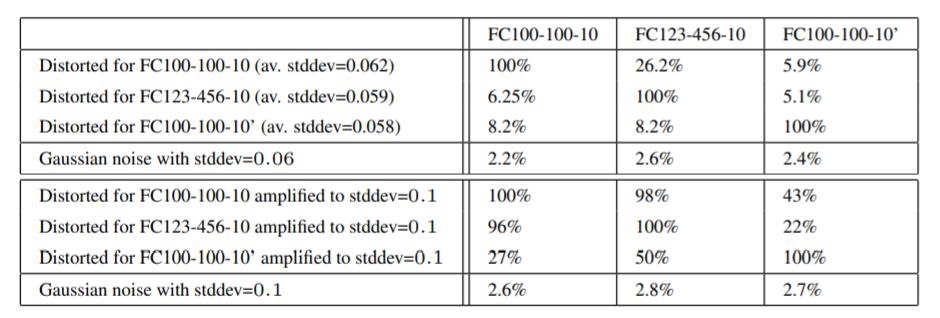
위의 Table 2와 동일한 역할을 한다.
다만 이 표에는 크게 두 개의 표가 있는데 그렇다면 밑에 것은 무엇인가? 왜곡의 정도를 magnify 했을 때의 결과이다.
[그렇다면 어떻게 이를 관리할 것인가? ]
upper 립시츠 bound를 두면 좀 더 다른 네트워크에 일반화가 잘 될 가능성을 제시한다.
+ 본 논문의 8-9 페이지를 참조하면 알 수 있다.
++ 립시츠 bound?
립시츠 연속 함수라는 게 있는데, 이건 두 점 사이의 거리를 일정 비 이상으로 증가시키지 않는 함수라고 한다. 흠 어렵군2
립시츠?!
립시츠............시카고에서 cell block tengo에 나오는 이름인데........... 시카고 한 번 더 보고 싶다.....ㅠㅠ 내가 돈 버는 건 오직 뮤지컬 때문...............
[결론]
직관적이지 않은 DNN의 속성들을 크게 두가지 살펴보았다.
개별 유닛의 의미와 그들의 불연속성과 관련된 속성들이었다.
왜 이런 adversariabl negative 이 나타나는지, 그리고 어떻게 이것들을 처리할 수 있는지 후속 연구에서 진행되어야 한다는 말로 마무리하고 있다.
[reference]
[0] Intriguing properties of neural networks https://arxiv.org/pdf/1312.6199
[1] The Expressive Power of Neural Networks: A View from the Width https://arxiv.org/abs/1709.02540
[2] https://ko.wikipedia.org/wiki/%EB%A6%BD%EC%8B%9C%EC%B8%A0_%EC%97%B0%EC%86%8D_%ED%95%A8%EC%88%98
- The expressive power describes neural networks’ ability to approximate functions. The celebrated universal approximation theorem states that depth-2 networks with suitable activation function can approximate any continuous function on a compact domain to any desired accuracy. [1] [본문으로]
- 위키를 참고했다. [2] [본문으로]
'딥러닝 > CV 논문' 카테고리의 다른 글
| [Classification]FuCiTNeT (0) | 2021.09.16 |
|---|---|
| [Generation]Generative Adversarial Nets (0) | 2021.08.23 |
| [Instance Segmentation] SOLO (0) | 2021.08.12 |
| [Object Detection] YOLO (0) | 2021.08.03 |
| [Classification] ViT: Vision Transformer (0) | 2021.07.29 |




댓글