https://hyelimkungkung.tistory.com/41?category=935163
[Generation]Generative Adversarial Nets
우왕! 이번엔 새로운 분야 이미지 생성이다! 하지만 난 그닥 흥미가 가지 않는다. 정말 재밌고 놀라운 걸 할 수 있는 분야인 건 확실한데........약간 그거다 불쾌한 골짜기..무서워....... 그리고 사
hyelimkungkung.tistory.com
[수학적 증명을 더 자세히 보자]
이 GAN 모델은 수학적 증명이 꽤 간단하게 나와있다. 머리를 데굴데굴 굴려서 무슨 말인지 이해해보자.
기본적으로 GAN 모델이 어떻게 굴러가는지는 알고 있다고 치겠다.
4.1 global optimality of $p_{g} = p_{data}$
Generator 가 어디로 수렴하는지 증명하는 부분이다.
1) 우선 Generator 가 주어진다고 가정한다. 이때 최적의 Discriminator는 $D^*_{G}(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)} $
왜 그런가?
G가 주어졌다면, value function은 maximize 하는 D를 찾기만 하면 된다.

V는 expectation의 합(확률 * 확률변수 값) 으로 이루어져 있으므로, 아래와 같이 표현할 수 있다.

위에서 아래로 변한 건 단순히 변수를 쓰는 방법만 변경해주었다.
이때, $log(D(x))$를 하나의 미지수 y로 치환하면, value function은 $\int alog(y) - blog(1-y)dy$로 바꿔쓸 수 있다.
우리가 원하는 건 Value function을 최대화하는 D 이기 때문에 위 식 = 0 을 만족하는 지점을 찾으면 된다.
$\int alog(y) - blog(1-y)dy = 0$ 을 풀면 극대점은 $\frac{a}{a+b}$로 나온다.
따라서 a에 $p_{data}(x)$, b에 $p_{g}(x)$를 넣는다면
$D^*_{G}(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)} $가 나온다.
2) 최적의 D 일때, value function은 $p_{g} = p_{data}$ 일때 최소값 -log4로 수렴한다
이제 최적의 G를 쓰기 때문에 Cost는 Generator에만 영향을 받도록 표기가 바뀐 것을 확인할 수 있다!
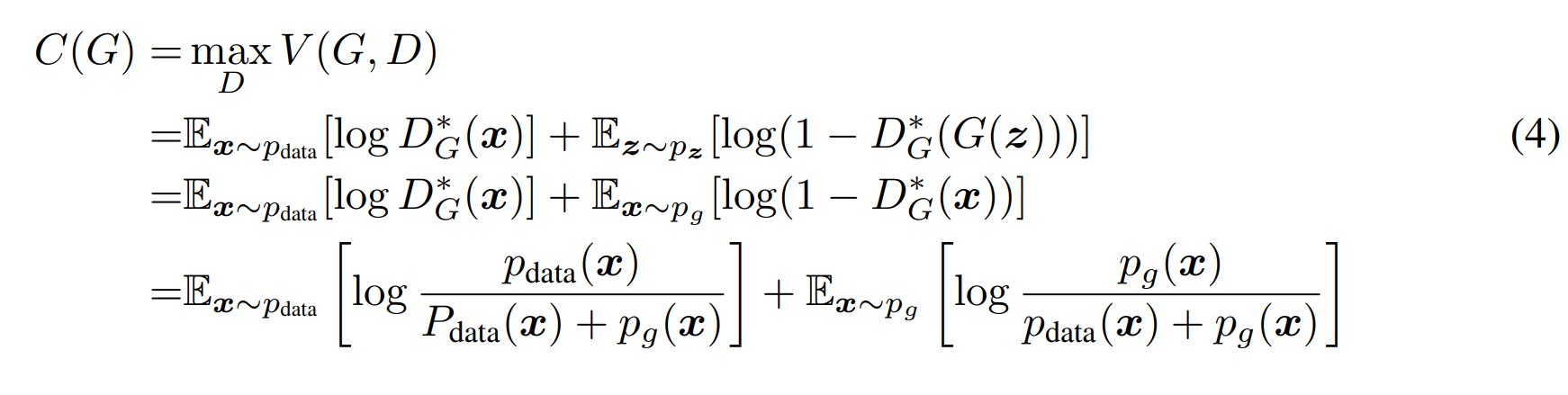
Value function에 $D^*_{G}(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)} $를 넣어준 것 말고는 변한게 없다.
이 값이 최소가 될때는 (max D가 끝났으니까 min G 할 차례) $p_{g} = p_{data}$일 뿐이고, 그때 최소값은 -log4 다.
그럼 어떻게 $p_{g} = p_{data}$ 이때가 최소인 걸 아느냐?
그걸 또 증명해 보면 되지
C(G)에서 -log4를 더 하고 빼 보자. (+value function을 다시 expectation을 확률*확률변수의 integral 값으로 변환)

여기서 갑자기 KL 이라는게 나온다.
쿨백 라이블러 발산(Kullback-Leibler divergence, 이하 KL)은 서로 다른 두 분포 사이의 차이를 계산한다.
즉 기존의 확률분포 P 가 있다고 했을 때, P를 모르기 때문에 우리가 샘플링 때 대신 사용하는 확률분포 Q 사이의 엔트로피 차이를 계산하는 함수이다.
계산 방법은 아래와 같다.
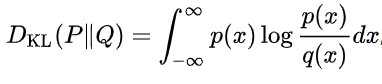
자세한 설명은 https://angeloyeo.github.io/2020/10/27/KL_divergence.html 여기 참조
이 함수를 잘 들여다 보고 있으면 위의 식에서 두 번째, 세 번째 term과 유사하게 생겼다.
즉 아래 식의 q(x)가 위 식 두번째 term의 $p_{data}+p_{g}$, p(x)가 위식 두번째 term의 $p_{data}$ 인 셈이다.
그걸 알고 나면 C(G) 함수는 아래와 같이 써진다.

이 식을 다시 JSD를 이용해서 정리하면 아래와 같이 변한다.
Jensen-Shannon divergence 는 KL가 유사하게 두 확률분포 사이의 유사도, 혹은 차이를 알 수 있는 지표이다.
다만 KL의 경우 symmetric 하지 않다.
따라서 이걸 symettric 하게 보정한 친구라고 보면 된다.

symmetric 하기 때문에 JSD(p,q) = JSD(q,p) 이다.
이 JSD 정의를 잘 보고 있으면 위의 5번 식이 또 다르게 보이지 않는가?
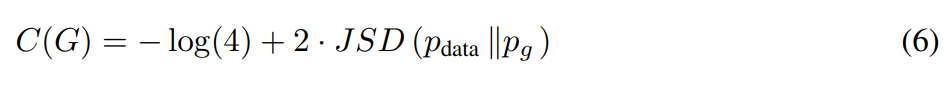
단 이때, JSD는 항상 양수의 값을 가지고, 0 의 값을 가질 때는 오직 $p_{data}$와 $p_{g}$가 동일해질 때 뿐이다.
따라서 C(G)는 항상 -log4 보다 크거나 같고, -log4 일때는 $p_{g} = p_{data}$ 뿐이다.
증명 끝 !
하지만 진짜 악마는 2번째
얘는 턱없이 짧게 써놓고...
4.2 Convergence of Algorithm 1

Generator가 수렴하는 건 알겠는데, 그래서 Algorithm 1을 쓰면 수렴하는거야? 에 답하는 부분.
우리가 여태껏 지지고 볶고 했던 Value function을 다시 보자.

이 V(G, D) = U($p_{g}$, D) 로 바꿔쓸 수 있다.
그렇다면 이때 U($p_{g}$, D) 는 $p_{g}$ 에 대해서는 convex 한 함수이다.
앞서서 V(G, $D^*$)는 $p_{g} = p_{data}$ 가 유일해이므로,
조금만 Generator를 업데이트 해도 충분히 수렴할 수 있다는 것이다 .
supD U(pg, D) is convex in pg with a unique global optima as proven in Thm 1, therefore with sufficiently small updates of pg, pg converges to px, concluding the proof.
'딥러닝 > CV 논문' 카테고리의 다른 글
| [NLP]Transformer_ver2 (3) | 2024.10.05 |
|---|---|
| [Instance Segmentation] Mask R-CNN (0) | 2022.08.01 |
| [Object Detection] Faster R-CNN (0) | 2022.07.27 |
| [Classification] ResNet 요약 (0) | 2022.07.10 |
| [Object Detection] CenterNet2 요약 (0) | 2022.03.21 |




댓글