[사족]
처음으로 읽어보고 접해보는 GNN 아키텍쳐! GNN 에 대해서 잘 모르기 때문에 이번 포스팅에서는 참고 문헌이 많다. 본격적으로 GCN에 대해 알아보기 전에 먼저 GNN의 기본 개념들을 훑고 가보자.
이 논문은 그림이 없다.
Semi-Supervised Classification with Graph Convolutional Networks
초록 Abstract
그래프에 직접적으로 이용할 수 있도록 convolutional neural network을 변형에서 그래프 기반 데이터에 적용하는 준지도학습 방법을 소개한다. 이는 기존의 spectral graph convolution의 localized 일차근사를 함으로써 얻어낸 구조이다. 지역적 그래프 구조와 노드의 피쳐들을 동시에 encode해서 히든 레이어에서는 표현하고, 모델은 레이어가 늘어남에 따라 시간복잡도는 선형적으로 늘어난다는 점에서 기존의 모델을 개선했다고 할 수 있다.
1. Introduction
그래프에서 node를 classification할 때 전체 데이터 셋에 비해 노드의 label이 달려있는 데이터가 드문 것이 자주 문제가 된다. 이를 해결하기 위해서 준지도 학습을 이용하는 것이며 동시에 graph Laplacian regularization term을 loss function에 추가해줌으로써 과적합을 막는다.
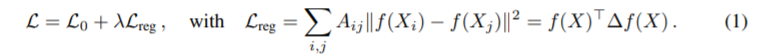
$L_{reg}$가 graph Laplacian regularization term 이다. 위에서 각각 기호들이 무엇을 의미하는지 한 번 살펴보자.
$f$ : neural-network 같은 미분가능한 함수
$X$ : 노드 피쳐 벡터들 (그러니까 일반 데이터셋으로 따지만 데이터 프레임)
$\bigtriangleup = D - A$ : unnormalized graph Laplacian of undirected graph
$A$ : 인접 행렬
$D$ : 차원 행렬
$f, X, A, D$는 [사족]에서 설명했으니 위에서 확인을 바라고 저 $\bigtriangleup $만 어떤 의미인지 한 번 같이 보도록 하자$
그런데 이렇게 계산하는 equation (1)은 연결된 노드들은 같은 label을 가질 것이라는 가정을 한다. 실제로, 이 가정은 모델의 수용력을 저해한다. 그래프 edged들이 연결됐다고 해서 node similarity를 encode하고 있지 않을 수도 있고, 또 추가적인 information을 담고 있을 수도 있기 때문이다.

그렇기에 본 논문에서는 그래프 구조에 직접적으로 이용할 수 있는 network model f(X,A)를 제안한다. 또한 훈련을 할 때도 레이블이 있는 노드로만 계산하는 supervised target $L_{0}$를 이용한다. 그럼으로써 위와 같이 그래프 기반으로 어떤 정규화를 거치는 과정을 겪지 않아도 된다.
크게 두 가지의 내용이 있는데, (1) 직접적으로 그래프에 적용할 수 있는 layer wise 한 간단하고 잘 작동하는 순전파 식을 만들고 (2) 이 순전파 식을 어떻게 GNN에 적용할지 를 다룬다.
2. Fast Approximate Convolutions on graphs
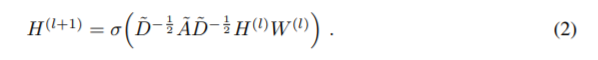
위와 같은 식을 통해서 GCN은 순전파를 진행한다. 그런데 가끔
$$ H^{(l+1)} = \sigma(AH^{(l)}W^{(l)}$ 이라는 식을 이용하는 사람들도 있던데, 이게 오히려 이해하기 편할 것 같다. 하지만 논문에서 저 식을 소개하니 저대로 따라가보도록 하자.
$A^{\tilda} = A + I_{N}$ : 인접 행렬에다가 identity 행렬을 더해준다.
2.1 Spectral graph convolutions
기존에 합성곱을 할 때 우리는 필터와 input 값을 곱함으로써 output을 계산하였다. 여기서도 마찬가지이다.

$g_{\theta}$가 filter인 셈이고, x가 노드의 값이다.
이때 오른쪽 식은 eigendecomposition을 통해서 얻어진다.
이게 기존에 소개된 방식인데 이 식의 문제는 무엇보다도 계산이 expensive 하다는 것이다. 시간 복잡도가 노드의 수의 제곱배로 늘어난다. 더욱이 큰 그래프에서는 eigendecomposition을 하는 것 자체가 너무나도 expensive 해진다. 따라서 이 문제를 해결하기 위해서 Hammond et al.(2011) 이 truncated expansion을 이용했다고 한다.

$T_{k}$는 통수 때 배웠던 taylor expansion과 유사한 것 같다.
Chebyshev expansion을 통해서 이제 filter를 근사시키는 것이다.
$T_{k} = sxt_{k-1}(x) - T_{k-2}(x), T_{0}(x) = 1, T_{1}(x) = x$
그래서 원하는 k 차수만큼 기존의 L을 근사하여 이용하게 된다.
=> 즉, K 만큼 거리에 있는 neighborhood 들만 다음 hidden layer의 output을 계산할 때 반영이 된다는 것을 의미한다.
여기서 conv layer와 유사한 의미를 가진다고 할 수 있다. K만큼의 receptive region을 이용해서 layer 계산한다는 의미에서!

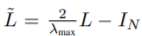
2.2 layer-wise linear model
아래에서부터는 K=1 이라고 가정하고 식을 전개한다.
앞에서 말했듯이, K만큼의 receptive filed가 생기고 이를 계속해서 중첩해나가면 전체 그래프를 볼 수 있다는 장점이 있다. 더불어 전체 그래프에서 parameter가 공유되기 때문에 굉장히 큰 그래프에도 local 정보를 과적합하지 않고서도 훈련을 할 수 있다는 장점이 있다.
위에 있던 식의 T를 전개하면 아래와 같이 된다.
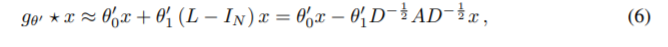
여기서 추가적으로 과적합을 피하고 연산 과정을 줄이기 위해서 아래와 같이 term을 일부 수정한다.
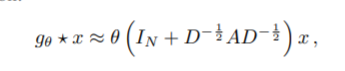
앞에서 우리가 $L^{\tilda}$를 계산할때 앞에 나눠주는 람다 term으로 인해서 위의 식은 [0,2]의 범위를 갖게 된다. 이는 레이어가 중첩됨에 따라서 기울기 소실 혹은 폭발이 일어날 수 있기 때문에 아래와 같이 다시 바꿔준다.
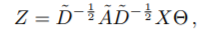
이를 통해서 O(|$\epsilon$|) 만큼의 복잡도가 가지기에 효율적으로 spase 한 행렬과 dense 한 행렬의 곱셈을 수행할 수 있다.
3. Semi-supervised node classification
그래서 순전파를 간단히 하면 아래를 통해서 식을 계산할 수 있다. 아래식은 사실 조금 적어보면 금방 이해할 수 있을 것이다. XW를 통해서 이제 계산을 한 후에 A를 곱해줌으로써 인접한 애들만 0 아닌 값이 들어가게 해주는 그런 방식이다.
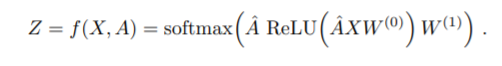
그림으로 표현하면

결국 $X_{2}$를 계산하는데 인접한 다른 노드들 역시 계산하였음을 알 수 있다.
4, 5 는 디테일한 사항이라 넘어간다.
'딥러닝 > 기타 리뷰' 카테고리의 다른 글
| [음성데이터] 음성데이터 개괄 (0) | 2022.07.11 |
|---|---|
| [Optimizer]AdamW (0) | 2022.02.10 |
| [의료데이터] 단백질 구조 예측 (0) | 2021.11.24 |
| [의료이미지 분석]Introduction to medical image analysis (0) | 2021.09.22 |
| [NLP] 토픽 모델링 - LSA, LDA 위주 (0) | 2021.07.29 |




댓글